CSS code
In quantum error correction, CSS codes, named after their inventors, A. R. Calderbank, Peter Shor and Andrew Steane, are a special type of Stabilizer codes constructed from classical codes with some special properties.
Construction
Let 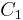 and
and 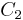 be two (classical)
be two (classical) ![[n,k_1]](/2012-wikipedia_en_all_nopic_01_2012/I/7871906e47984be86355ba212e289f09.png) ,
, ![[n,k_2]](/2012-wikipedia_en_all_nopic_01_2012/I/2b6a22719f7c3861e65fe981e5eb5aaa.png) codes such, that
codes such, that 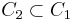 and
and 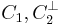 both have minimal distance
both have minimal distance 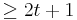 , where
, where 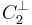 is the code dual to
is the code dual to 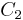 . Then define
. Then define 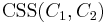 , the CSS code of
, the CSS code of 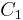 over
over 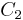 as an
as an ![[n,k_1 - k_2, d]](/2012-wikipedia_en_all_nopic_01_2012/I/d85c8b7b6899e757949b2f78eaf9c7e5.png) code, with
code, with 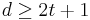 as follows:
as follows:
Define for 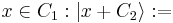
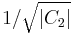
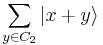 , where
, where 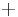 is bitwise addition modulo 2. Then
is bitwise addition modulo 2. Then 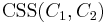 is defined as
is defined as 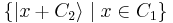 .
.
References
Michael A. Nielsen and Isaac L. Chuang (2010). "Quantum Computation and Quantum Information (10. Anniversary Edition)". Cambridge University Press.